Часть 2. Как выбрать микроцель для обучения

Статистика оценок или почему не надо испольлзовать только метод проверки значимости нулевой гипотезы, основанный на p-value.

Реклама
Анализ данных
Автор

Александр Коршаков

Дата публикации

29 июля 2024 г.

Напомню, что в первой части статьи мы прошли шаги:

  1. Подготовка данных к корреляционному анализу.
  2. Корреляционный анализ макро- и микроцелей.
  3. Регрессионный анализ и предективная аналитика.
  4. Сбор данных: обучаем стратегию показов в Яндекс Директ.

Данные собраны. Остался последний шаг — провести post-hoc тест и оценить эффективность обучения стратегии на выбранной микроцели.

Не пропускайте выход новых статей!

Подписывайтесь на мой ТГ-канал DDM & Ads


Проблема статистики на основе p-value и преимущества оценочных методов

Проверка значимости нулевой гипотезы (Null Hypothesis Significance Testing, NHST) часто применяется в маркетинговых исследованиях, но этот метод ограничен. Он отвечает только на вопрос: «Есть ли эффект?». В экономиках и социальных науках вместо NHST используют оценочные методы. Например, указывают: «средний доход составил 50 000₽ ± 1500₽».

  1. Проблема с интерпретацией p-value. p-value часто неправильно интерпретируется как вероятность гипотезы или вероятность того, что нулевая гипотеза неверна. На самом деле, p-value — это вероятность наблюдения данных, которые были бы столь же экстремальными, если нулевая гипотеза была верна.

  2. Чувствительность к объёму выборки. p-value может стать очень маленьким при больших объёмах выборки, даже если эффект, который он измеряет, незначителен с практической точки зрения. Это может привести к ложным заключениям о значимости результатов.

  3. Множественные тесты и проблема множественных сравнений. При проведении множества тестов на одной выборке вероятность получения хотя бы одного ложного положительного результата увеличивается. Это может привести к увеличению числа ложных положительных результатов (ошибки первого рода).

  4. Отсутствие информации о размере эффекта. p-value не сообщает о размере эффекта или его практической значимости, а только о том, насколько результаты отклоняются от нулевой гипотезы.

  5. Зависимость от выбранного уровня значимости. Выбор порогового значения для p-value (например, 0.05) является произвольным и может влиять на интерпретацию результатов. Это может привести к субъективности в принятии решений о значимости.

  6. Игнорирование контекста и практической значимости. Исследователи могут сосредоточиться только на том, чтобы p-value было ниже уровня значимости, не принимая во внимание контекст исследования или практическую значимость результатов.

  7. Проблемы с повторяемостью. Результаты, которые основываются только на p-value, могут быть трудно воспроизводимыми. Это связано с тем, что даже небольшие изменения в данных могут значительно повлиять на p-value.

Эти проблемы подчеркивают необходимость использования более комплексных методов статистического анализа, таких как оценка эффектов, доверительные интервалы и байесовские методы, которые могут предоставить более полную картину исследуемых данных.

Оценочные методы более информативны. Они дают не только факт наличия эффекта, но и его величину и вариации. Смещение акцента с NHST на оценку эффектов и доверительных интервалов позволяет принимать более точные и обоснованные решения. Вместо простого факта наличия эффекта от рекламной кампании можно узнать его точные параметры, что помогает эффективнее планировать и оценивать стратегии.

Статистика оценок, также известная как оценочные методы или методы оценивания, предлагает несколько ключевых преимуществ по сравнению с традиционными подходами, такими как p-value. Вот основные преимущества:

  1. Предоставляет информацию о размере эффекта. Оценочные методы дают числовое представление о размере эффекта или его значимости, что позволяет лучше понять практическое значение результатов. Например, оценки могут включать в себя такие метрики, как разница средних значений, коэффициенты корреляции или регрессионные коэффициенты.

  2. Использует доверительные интервалы. Вместо того чтобы полагаться на p-value, оценочные методы часто используют доверительные интервалы, которые дают диапазон возможных значений для параметра. Это помогает понять точность и надежность оценок.

  3. Учитывает размер выборки и вариацию данных. Оценочные методы учитывают объем выборки и вариацию данных, что позволяет более точно интерпретировать результаты и избегать переоценки значимости.

  4. Подходит для множественных сравнений. Методы оценивания могут быть адаптированы для обработки множественных сравнений с использованием корректировок, таких как коррекция Бонферрони или метод ложных открытий (FDR), что снижает риск ложных положительных результатов.

  5. Предоставляет полное представление о данных. Вместо того чтобы сосредоточиваться на одном числовом значении (p-value), оценочные методы предоставляют полное представление о данных, включая эффекты, их размеры и их вариацию.

  6. Адаптируется к различным типам данных и моделей. Оценочные методы гибки и могут использоваться для анализа данных различных типов и сложных моделей, таких как линейные и нелинейные модели, модели с несколькими переменными и байесовские модели.

  7. Снижает риск ошибки интерпретации. Использование оценки и доверительных интервалов может снизить риск ошибок интерпретации, связанных с неправильным пониманием p-value, и дать более ясное представление о значимости и надежности результатов.

  8. Фокус на предсказательной способности. Оценочные методы могут сосредоточиться на оценке предсказательной способности модели, что важно для практических применений, таких как прогнозирование и принятие решений.

Эти преимущества делают статистику оценок полезным инструментом для более глубокого и точного анализа данных, особенно в ситуациях, когда требуется точное понимание эффектов и их значимости.

В этой статье рассмотрим плюсы и минусы графиков на основе p-value. Познакомимся с оценочным графиком Гарднера-Альтмана, который приходит на смену устаревшим методам на основе p-value.


Подготовка и обзор данных

Проведем анализ эффективности работы двух микроцелей сравнив результаты с контрольным периодом.

  • Анализируемые периоды:
    1. Контрольный с 01.04.24 по 14.04.24 — период работы стратегии «Максимум кликов».
    2. Тестовый 1 с 15.04.24 по 28.04.24 — период работы цели «dl6».
    3. Тестовый 2 с 27.05.24 по 9.06.24 — период работы цели «m6».
Загрузка библиотек 
# обработка данных
library(data.table)
library(dplyr)

# вывод интерактивных таблиц
library(DT)

# графика
library(ggplot2)

# статистика на графиках
library(ggsignif)

# статистика оценок
library(dabestr)


Описательные статистики данных

Код 
data %>%
  group_by(Per) %>%
  summarise(psych::describe(Goals, skew = FALSE)) |> 
  datatable(
    rownames = FALSE,
    class   = 'display compact nowrap',
    options = list(dom  = 't')) |> 
  formatRound(columns = c(4,5,10), digits = 2)


Как понять эффективность микроцели?

Собственно, а как понять, что микроцели сработали лучше, чем контрольный период? Ответ прост: нам нужно сравнить средние значения выборок.

Мы можем легко вычислить среднюю разницу в наблюдаемых выборках. Это и есть наша оценка интересующего нас размера генерального эффекта.

Но как мы можем определить точность и уверенность нашей оценки? Можем ли мы понять, как она соотносится со средней генеральной разницей?

Мы можем рассчитать 95%-ный ДИ средней разницы, выполнив бутстрап-выборку. Впервые описанный Брэдли Эфроном, бутстрап - это простая, но мощная техника. Он создает несколько выборок (с заменой) из одного набора наблюдений и рассчитывает размер интересующего эффекта по каждой из этих выборок. Затем бутстрап-выборки величины эффекта можно использовать для определения 95%-ного CI.

Сравнение средних значений двух выборок на первый взгляд может показаться простым, но для получения надежных и корректных результатов необходимо учитывать несколько важных факторов:

  • Размер выборки (Sample Size):
    • Большие выборки могут давать более точные оценки среднего значения и его разброса. Малые выборки могут быть подвержены случайным колебаниям, что делает результаты менее надежными.
  • Разброс (Variance):
    • Разброс значений в выборках должен быть учтен, так как даже при одинаковых средних значениях, выборки с различным разбросом могут иметь разные статистические характеристики.
  • Дисперсия (Variance) и стандартное отклонение (Standard Deviation):
    • Эти показатели показывают степень разброса данных относительно среднего. Сравнение двух средних значений без учета их дисперсий может быть вводящим в заблуждение.
  • Независимость данных (Independence of Data):
    • Выборки должны быть независимыми друг от друга. Если между ними существует зависимость, это необходимо учитывать при анализе.
  • Статистическая значимость (Statistical Significance):
    • Нужно учитывать вероятность того, что наблюдаемые различия в средних значениях возникли случайно. Это обычно проверяется с помощью тестов значимости, таких как t-тест.
  • Конфиденциальные интервалы (Confidence Intervals):
    • Они показывают диапазон, в котором с определенной вероятностью находится истинное среднее значение. Это дает более полное представление о точности оценки.
  • Практическая значимость (Practical Significance):
    • Даже если различие статистически значимо, важно оценить его практическую значимость и влияние на реальную ситуацию.

Что мы можем НЕ учитывать в оценочной статистике (её еще называют «новой статистикой»)

  • Нормальность распределения (Normality of Distribution):
    • Многие статистические тесты предполагают, что данные распределены нормально. Если это не так, могут потребоваться непараметрические методы или преобразование данных.
    • В новом подходе мы многократно извлекаем выборку из ген. совокупности (5 000 раз), что дает нормальное распределение средних значений.
  • Уровень значимости (Significance Level, p-value):
    • Определяет вероятность того, что наблюдаемые различия являются случайными. Обычно используются пороговые значения, такие как 0.05.
  • Типы ошибок (Types of Errors):
    • Ошибка первого рода (Type I Error): Отказ от нулевой гипотезы, когда она верна.
    • Ошибка второго рода (Type II Error): Принятие нулевой гипотезы, когда она ложна.

Но сначала рассмотрим стандартные графики, на основе которых специалисты принимают решение о результатах тестирования.

Гистограмма со звёздочкой

Гистограмма средних значений co звёздочкой

Код 
# вычисление средних значений и стандартных ошибок
summary_data <- data |>
  _[, .(
    mean = mean(Goals),
    se = sd(Goals) / sqrt(.N)),
    by = Per
    ]

# создание barplot для первого периода
ggplot(
  summary_data, 
  aes(x = Per, y = mean, fill = Per)
  ) +
  geom_bar(
    stat = "identity", 
    position = position_dodge(),
    width = 0.7
    ) +
  geom_errorbar(
    aes(ymin = mean - se, ymax = mean + se), 
    width = 0.2, 
    position = position_dodge(0.7)
    ) +
  scale_fill_manual(
    values = c(
      "Control" = "#17BECF", 
      "Test 1" = "#E377C2",
      "Test 2" = "#9467BD"
      )) +
  theme_minimal() +
  labs(
    x = "Group", 
    y = "Mean Value") +
  theme(
    legend.position = "none",
    axis.title = element_text(size = 12, color = "gray50"),
    axis.text = element_text(size = 10, color = "gray50"),
    panel.grid = element_blank(),
    plot.margin = ggplot2::margin(
      t = 0.3,
      r = 0.3, 
      b = 0.3,
      l = 0.3, 
      "cm"
      ))+
  geom_signif(
    comparisons = list(
      c("Control", "Test 1"),
      c("Control", "Test 2")),
    map_signif_level = TRUE
    )

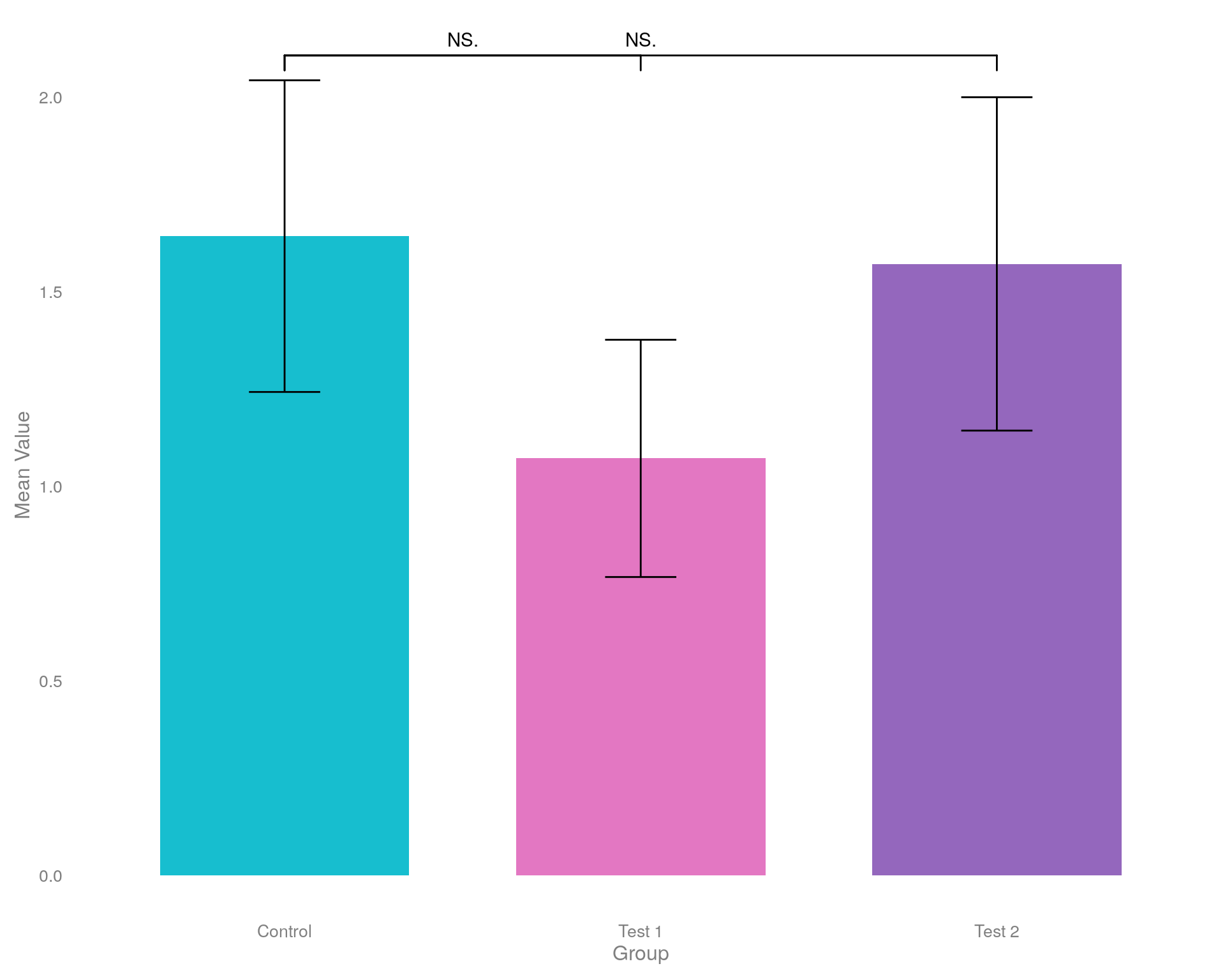
Что мы видим на этом графике?

  • средние значения с учетом стандартной ошибки (SE)
  • выводы о значимости «p-value». В нашем случаи на графике мы видим значение «NS», означает, что значение «p-value» не достигает уровня значимости, часто принимаемого как 0.05, то есть p >= 0.05.

Что мы НЕ видим?

  • График не показывает конкретные данные, используемые для его построения, что затрудняет понимание вариабельности данных.
  • Неизвестно, насколько сильно отличаются средние значения между группами. Это важно для интерпретации значимости различий.
  • Непонятно, насколько точно оценен размер эффекта, что может быть важно для понимания достоверности различий.
  • График не показывает доверительный интервал (CI) или вероятность того, что размер эффекта истинный. Это важно для интерпретации надежности результата.
  • Создает ложную дихотомию с «звездочкой значимости». – Использование звездочки для обозначения значимости может создать впечатление, что различия либо значимы, либо нет, игнорируя степень и важность этих различий. Это упрощает сложность данных и создает ложное представление о результатах.

Ложная дихотомия, или ложная дилемма, в статистике и логике – это ошибка рассуждения, при которой представляется ситуация, как будто существует только два взаимоисключающих варианта, хотя на самом деле их может быть больше. В контексте статистики ложная дихотомия может приводить к неверным выводам и анализу данных.

Примеры ложной дихотомии:

  • «Либо данные показывают, что эффект существует, либо они не показывают ничего.» Это утверждение игнорирует возможность того, что данные могут быть недостаточно мощными для выявления эффекта.

  • «Либо корреляция равна нулю, либо она значительна.» В реальности существуют значения корреляции, которые могут быть слабыми и незначительными, но все же не нулевыми.

Важно избегать ложной дихотомии при анализе данных, чтобы не упрощать сложные ситуации и не упускать важные детали, которые могут оказать влияние на результаты и выводы исследования.

Boxplot

Используем прямоугольную диаграмму (boxplot) для визуализации данных.

График: Boxplot

Код 
# включаем отображение текста на графике
# showtext_auto()

ggplot(
  data, 
  aes(
    x = Per, 
    y = Goals,
    fill = Per
    )
  ) + 
  geom_boxplot(outlier.colour = "tomato2") + 
  scale_fill_manual(
    values = c(
      "Control" = "#17BECF", 
      "Test 1" = "#E377C2",
      "Test 2" = "#9467BD"
      )) +
  theme_minimal()+
  labs(
    x = "Group",
    color = NULL
    )+
  theme(
    legend.position = "none",
    axis.title = element_text(size = 14, color = "gray50", family = "roboto"),
    axis.text = element_text(size = 12, color = "gray50", family = "roboto"),
    plot.margin = ggplot2::margin(
      t = 0.3,
      r = 0.3, 
      b = 0.3,
      l = 0.3, 
      "cm"
      ))+
  geom_signif(
    comparisons = list(
      c("Control", "Test 1"),
      c("Control", "Test 2")),
    map_signif_level = TRUE
    )

Код 
# отключаем отображение текста на графике
# showtext_auto(FALSE)

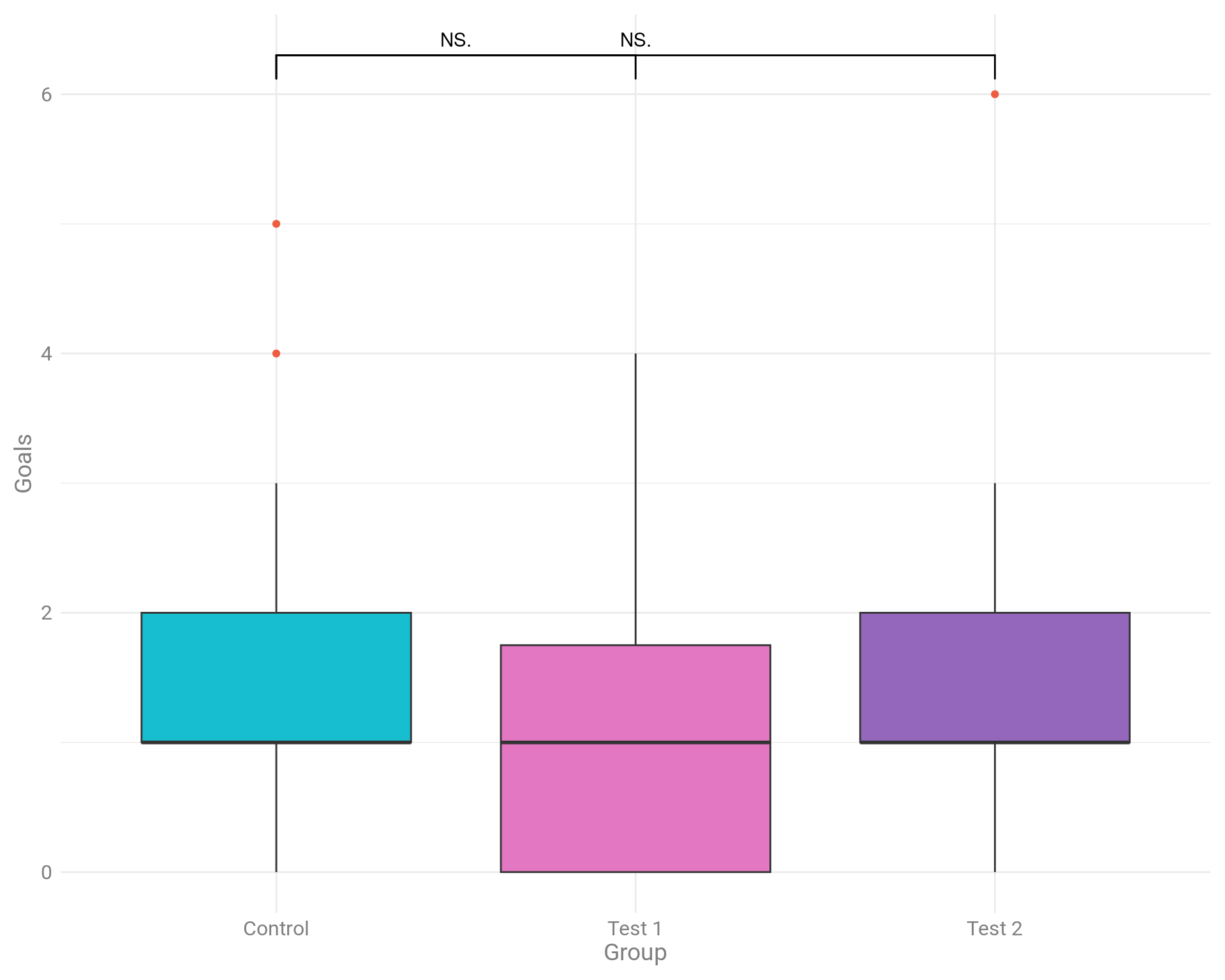
Что мы видим на графике boxplot?

  • медиану, квартили, выбросы, минимальное и максимальное значение;
  • выводы о значимости «p-value».

На диаграмме по-прежнему отображаются не все данные. Нам по-прежнему не хватает информации о базовом распределении данных. Они распределены нормально? Есть ли перекос в точках? Каков размер выборки? Что еще более важно, на диаграммах не отображается размер эффекта.

Jitter plot

Для отображения нескольких точек данных по одной или нескольким категориям мы можем использовать график «Jitter».

График: Jitter plot

Код 
ggplot(
  data, 
  aes(
    x = Per, 
    y = Goals,
    colour = Per
    )
  ) + 
  geom_jitter() + 
  scale_color_manual(
    values = c(
      "Control" = "#17BECF", 
      "Test 1" = "#E377C2",
      "Test 2" = "#9467BD"
      )) +
  theme_minimal()+
  labs(
    x = "Group",
    color = NULL
    )+
  theme(
    legend.position = "none",
    axis.title = element_text(size = 10, color = "gray50"),
    axis.text = element_text(size = 9, color = "gray50"),
    plot.margin = ggplot2::margin(
      t = 0.3,
      r = 0.3, 
      b = 0.3,
      l = 0.3, 
      "cm"
      ))+
  geom_signif(
    comparisons = list(
      c("Control", "Test 1"),
      c("Control", "Test 2")),
    map_signif_level = TRUE, 
    color ="black"
    )

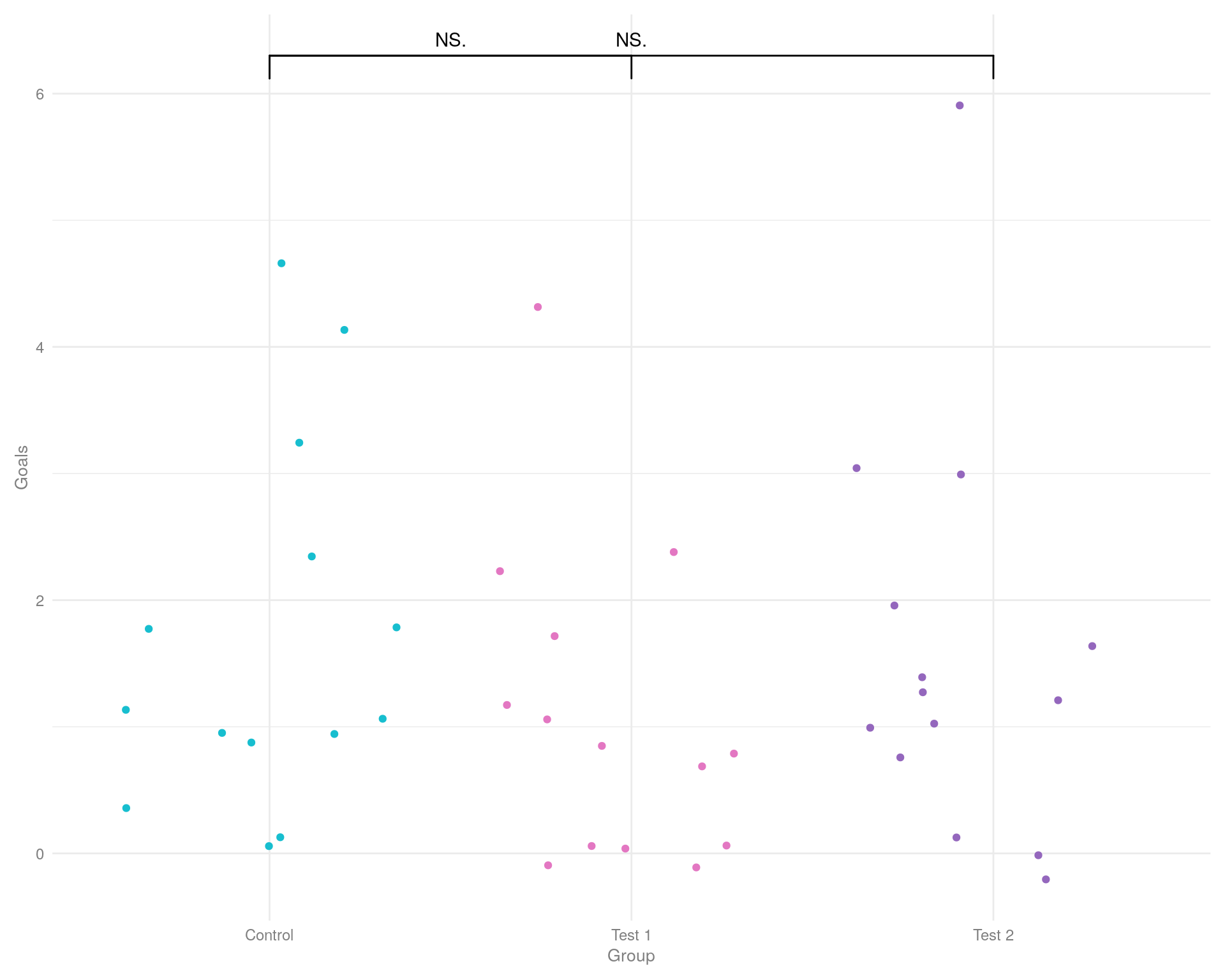
Графики «дрожания» позволяют избежать перекрытия точек данных (т. е. точек данных с одинаковым значением по оси «y») путем добавления случайного коэффициента к каждой точке вдоль ортогональных осей «x». Таким образом, хотя график дрожания отображает все точки данных (неявно указывая визуально размер выборки), он может неточно отображать базовое распределение данных.

И по-прежнему мы видим не все, что нам необходимо для принятия решения о внедрении микроцели для обучения стратегии.

Есть проект, в котором я буду полезен?

Обращайтесь! Контакты


График Гарднера-Альтмана

Теперь мы создадим график без проблем, о которых говорилось ранее.

С помощью пакета «dabest» мы сгенерируем данные о средних значениях и создадим 95% доверительный интервал методом бутстрапа, используя 5000 выборок.

Бутстрап-выборка даёт нам два важных преимущества:

  • Непараметрический статистический анализ. Не нужно предполагать, что наши данные или базовые популяции имеют нормальное распределение. Согласно центральной предельной теореме, распределение размера эффекта при повторной выборке будет приближаться к нормальному.

  • Легко построить 95% доверительный интервал на основе распределения выборки. Для 1000 бутстреп-выборок средних разниц можно использовать 25-ю и 95-ю разницы в ранжированном списке как границы 95% доверительного интервала. Этот тип интервала называется интервалом перцентиля.

Оценочный график Гарднера-Альтмана

Код 
# подготовка данных к проведению теста 1
dabest_obj_1 <- data |> 
  dabestr::load(
    x = Per,
    y = Goals,
    idx = c("Control", "Test 1")
  ) |> 
  mean_diff()

# подготовка данных к проведению теста 2
dabest_obj_2 <- data |> 
  dabestr::load(
    x = Per,
    y = Goals,
    idx = c("Control", "Test 2")
  ) |> 
  mean_diff()


# создаем график для Тест 1
plot_dabest_obj_1 <- dabest_plot(
  dabest_obj_1, 
  float_contrast = TRUE, 
  custom_palette = "npg"
  )

# создаем график для Тест 2
plot_dabest_obj_2 <- dabest_plot(
  dabest_obj_2, 
  float_contrast = TRUE, 
  custom_palette = "npg"
  )

# выводим графики в одну строку и две колонки
cowplot::plot_grid(
  plotlist = list(plot_dabest_obj_1, plot_dabest_obj_2),
  nrow = 1,
  ncol = 2,
  labels = "AUTO"
  )

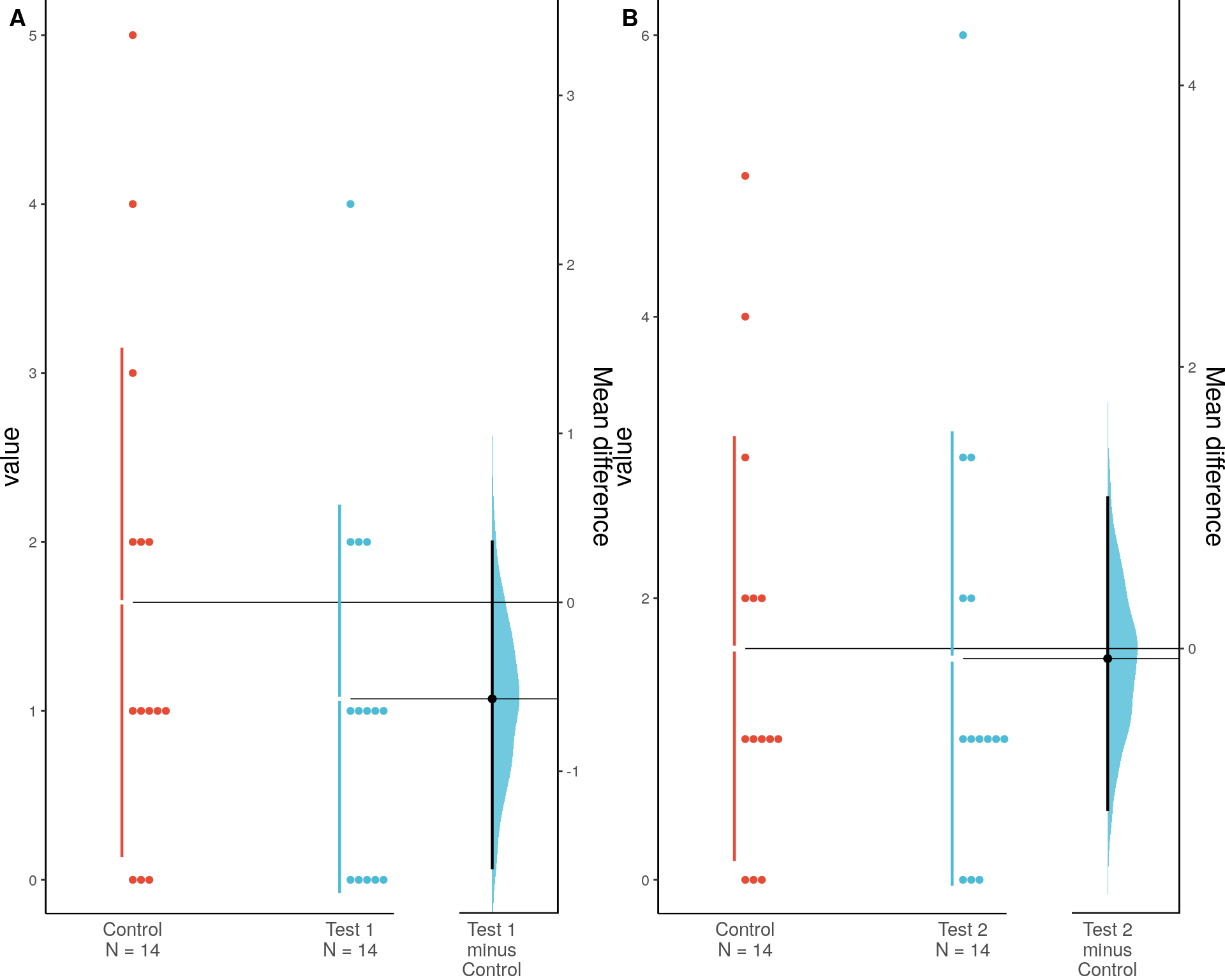
График оценки имеет две ключевые особенности:

  1. Все точки данных представлены в виде роевой диаграммы, которая упорядочивает каждую точку для отображения основного распределения.

  2. Величина эффекта представлена в виде бутстрепного 95% доверительного интервала (95% CI) на отдельных, но выровненных осях, где величина эффекта отображается справа от исходных данных, а среднее значение тестовой группы выравнивается с величиной эффекта.

В результате проведенных тестов мы получим следующий вывод для Control и Test 1:

The unpaired mean difference between Test 1 and Control is -0.571 [95%CI -1.571, 0.357]. The p-value of the two-sided permutation t-test is 0.3036, calculated for legacy purposes only. 5000 bootstrap samples were taken; the confidence interval is bias-corrected and accelerated. Any p-value reported is the probability of observing the effect size (or greater), assuming the null hypothesis of zero difference is true. For each p-value, 5000 reshuffles of the control and test labels were performed.

Таблица статистик для графика A: Контрольные и Тестовый 1 (цель «dl6»)


И выводы для Control и Test 2:

The unpaired mean difference between Test 2 and Control is -0.071 [95%CI -1.143, 1.071]. The p-value of the two-sided permutation t-test is 0.8483, calculated for legacy purposes only. 5000 bootstrap samples were taken; the confidence interval is bias-corrected and accelerated. Any p-value reported is the probability of observing the effect size (or greater), assuming the null hypothesis of zero difference is true. For each p-value, 5000 reshuffles of the control and test labels were performed.

Таблица статистик для графика B: Контрольные и Тестовый 2 (цель «m6»)


Переведем на человеческий на примере контрольной и тестовой выборки 1.

Результаты:

  1. The unpaired mean difference between Test 1 and Control is -0.571 [95%CI -1.571, 0.357].
    • Unpaired mean difference: Это средняя разница между двумя группами (Test 1 и Control). В данном случае, средняя разница составляет -0.571, что означает, что в среднем значения в группе Test 1 на 0.571 меньше, чем в группе Control.
    • 95%CI [-1.571, 0.357]: Это 95% доверительный интервал для средней разницы. Это означает, что мы уверены на 95%, что истинная средняя разница между группами лежит в интервале от -1.571 до 0.357.
  2. The p-value of the two-sided permutation t-test is 0.3036, calculated for legacy purposes only.
    • P-value: Это вероятность получить наблюдаемую разницу (или более экстремальную), если на самом деле между группами нет разницы (нулевая гипотеза верна). В данном случае, p-value составляет 0.3036.
    • Two-sided permutation t-test: Это тип статистического теста, используемый для сравнения двух групп. Он оценивает, есть ли значимая разница между ними.
    • Legacy purposes: Это означает, что p-value предоставлен для исторической значимости, но основное внимание уделяется другим метрикам (например, доверительным интервалам).
  3. 5000 bootstrap samples were taken; the confidence interval is bias-corrected and accelerated.
    • Bootstrap samples: Это метод повторной выборки, который позволяет оценить распределение статистики (например, средней разницы). В данном случае было взято 5000 выборок.
    • Bias-corrected and accelerated: Это тип коррекции доверительного интервала, который улучшает точность оценки.
  4. Any p-value reported is the probability of observing the effect size (or greater), assuming the null hypothesis of zero difference is true.
    • P-value: Это вероятность получить наблюдаемую разницу (или более экстремальную), если между группами на самом деле нет разницы (нулевая гипотеза верна).
  5. For each p-value, 5000 reshuffles of the control and test labels were performed.
    • Reshuffles: Это перестановки меток групп (Control и Test 1) для оценки распределения p-value. В данном случае было выполнено 5000 перестановок.

Вывод для цели «dl6»

Средняя разница между группами Test 1 и Control составляет -0.571. Доверительный интервал показывает, что истинная разница может лежать в диапазоне от -1.571 до 0.357. P-value составляет 0.3036, что означает, что наблюдаемая разница не является статистически значимой (мы не можем уверенно сказать, что есть разница между группами). Эти результаты основаны на 5000 повторных выборках и перестановках.

На основании данных нельзя с уверенностью сказать, что между группами Test 1 и Control существует значимая разница. Однако, доверительный интервал предоставляет полезную информацию о возможном диапазоне истинной разницы.

Вывод для цели «m6»

Средняя разница между группами Test 2 и Control составляет -0.071. Доверительный интервал показывает, что истинная разница может лежать в диапазоне от -1.143 до 1.071. P-value составляет 0.8483, что означает, что наблюдаемая разница не является статистически значимой (мы не можем уверенно сказать, что есть разница между группами). Эти результаты основаны на 5000 повторных выборках и перестановках.

На основании данных нельзя с уверенностью сказать, что между группами Test 2 и Control существует значимая разница. Однако, доверительный интервал предоставляет полезную информацию о возможном диапазоне истинной разницы.

Итог

На основе проведенных тестов мы можем смело заключить, что ни одна микроцель не подходит для обучения стратегии показов рекламных объявлений. Значит, продолжаем искать новые микроцели, но до тех пор показываем рекламу по стратегии «Максимум кликов».

Есть проект, в котором я буду полезен?